

Step 1: Solve one equation for one of the variables. Solving systems of equations using the substitution method involves replacing a variable in one equation with the equivalent of that variable, calculated using. When we use this method we solve one equation for one of the variables. Solving systems of equations by substitution follows three basic steps. So we substitute what y is equal to in terms of x into the first equation, thus being able to solve for x. Another alternative to solve a linear system is known as the substitution method. The approach is very simple: 1) Choose one of the two equations, for which it is easy to solve for any x.

Here, we see that the second equation has already been solved for one of the variables, that variable being y. How do you solve system of equations by substitution. Substitute that solution into either of the original equations. Substitute the expression for this variable into the second equation, then solve for the remaining variable. Solve one of the two equations for one of the variables in terms of the other. To solve for the system by the substitution method, we take one of the equations and solve it for either variable (x= or y=) then substitute this into the other equation. How To: Given a system of two equations in two variables, solve using the substitution method. In the second equation y is not multiplied by a constant so it can be isolated in fewer steps.The system consists of the following equations: 4x + 2y = -2 and y = 6x - 5 Substitution Method, The substitution method is most useful for systems of 2 equations in 2 unknowns. Solving Systems of Equations by Substitution Date Period Solve each system by substitution. Step 2: Then substitute the expression for that. x,\ y,\ or\ z x, y, or z) in one equation.
Substitution equation systems how to#
Here is the detailed strategy for how to solve systems of equations with three variables. The first step would be to choose one of the equations and solve it for either x or y. System of linear equations with three equations in three unknowns can be solved by making two substitutions. It does not matter which equation you choose first, or which variable you solve for first the values for both variables will be the same.įor example, given the system of linear equations: This method works by solving one of the linear equations for one of the variables, then substituting this value for the same variable in the other linear equation and solving for the other variable. Substitute the value found into any equation involving both variables and solve for the other variable.
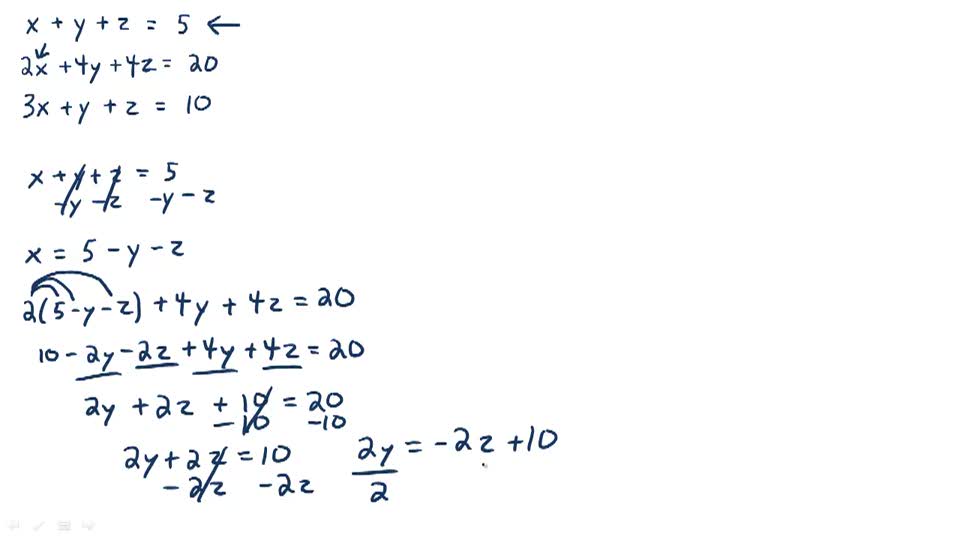

In the other equation, substitute for the variable just solved. vec itpp::lssolveud (const mat &A, const vec &b) Solves overdetermined linear equation. To solve systems using substitution, follow this procedure: Select one equation and solve it for one of its variables. bool itpp::lssolveud (const mat &A, const vec &b, vec &x) Solves underdetermined linear equation systems. cmat itpp::lssolveod (const cmat &A, const cmat &B) Solves overdetermined linear equation systems. To solve a system of linear equations without graphing, you can use the substitution method. Solves overdetermined linear equation systems.


 0 kommentar(er)
0 kommentar(er)
